Frances M. Aponte Caraballo
Department of Biology
UPR Cayey

Andrea B. Mercado Cabrera
Department of Biology
UPR Cayey

Abstract

COVID-19 disease is caused by a SARS-CoV-2 virus infection. Different countries have implemented interventions with mitigation strategies to manage the pandemic. In Puerto Rico, several executive orders and different resources have been implemented to contact trace and cut transmission chains of the virus while using non-pharmaceutical intervention. The proposed mathematical model is aimed to model the disease dynamics and analyze the mitigation strategies used to stop the spread of the virus locally. When incorporating vaccinations, the epidemic curve decreased as well as the effective reproductive number.

Keywords: COVID-19, epidemiological model, mitigation, interventions, vaccines

Resumen

El COVID-19 es una enfermedad causada por el virus SARS-CoV-2 que fue declarada pandemia. Alrededor del mundo, se han implementado diferentes medidas para mitigar los efectos de la pandemia. En Puerto Rico, se han incorporado órdenes ejecutivas y se ha realizado rastreo de casos tanto como intervenciones no farmacológicas para el control y manejo de los casos. Este estudio propone un modelo epidemiológico para estudiar la dinámica poblacional y las estrategias de mitigación implementadas. Los resultados preliminares indican que al aplicar medidas menos restrictivas hubo un aumento en casos. Tras incorporar las vacunas, la curva epidémica disminuyó junto con el número de reproducción efectivo.

Palabras claves: COVID-19, modelos epidemiológicos, mitigación, intervenciones, vacunas

Introduction

COVID-19 is an acute respiratory disease caused by the SARS-CoV-2 virus (Wang, et al., 2020). The virus has spread worldwide without discriminating by gender or age. It was declared a pandemic on March 11, 2020 (WHO, 2020a). This novel virus can be primarily transmitted by direct contact with an infected individual or with infected secretions such as saliva or respiratory droplets expelled when an infected person coughs, sneezes, talks, or sings (CDC 2020a; WHO, 2020b;). Other transmission methods are possible but not at the same infection rate (WHO, 2020b).

Once exposed to the virus, to become infected, the expected incubation period is 2-14 days (Lofti et al., 2020; Wiersigna et al., 2020;). Past the 2-14 days, this individual can either be symptomatic or asymptomatic (Han et al., 2020). The common symptoms among individuals are fever, dry cough, or fatigue (WHO, 2020c). By May 1, 2021, there were 152,788,245 confirmed cases and 3,205,783 deaths (Worldometer, 2021) worldwide; of these 116,180 confirmed cases and 2,310 deaths were from Puerto Rico (PDOH, 2021). As the epidemic progressed, treatments have become available; Remdesivir, Dexamethasone, Monoclonal Antibodies, and plasma transfusion are examples. The treatment given depends on the patient’s physical condition (Harvard Health Publishing, 2021).

This study proposes an epidemiological mathematical model to study the disease dynamics in a susceptible population and how mitigation strategies like mask usage, vaccines, and social distancing, when in use, help to manage the epidemic. “Without proper control, diseases can lead to widespread outbreaks and be harmful to public health. Fortunately, there are many methods available to contain diseases” (National Geographic Society, 2019). Interventions are applied depending on the strategy to be implemented or targets deemed necessary for the disease under study (CDC, 2020b). The possible kinds of strategies are mitigation or suppression strategies.

The Imperial College COVID-19 Response team states that mitigation strategies are not focused on stopping a spread but rather on slowing it (2020). The objective is to “flatten the curve” to minimize new infections. An example of a mitigation strategy is social (physical) distancing. As individuals are apart, the transmission rate decreases because there is no effective contact to continue the chain of transmission. This intervention extends the longevity of the epidemic but prevents saturation of the hospital systems. In the case of suppression strategies, the primary objective is to decrease the epidemic radically until it ends. “The challenge of this approach is that the Non-pharmaceutical Interventions (NPIs) need to be maintained, at least intermittently, for as long as the virus is circulating in the population, or until a vaccine becomes available” (Ferguson et al., 2020). Regardless of the type of strategies applied, whether it be mitigation or suppression, it is crucial to combine the preventive measures with the rest of the interventions, such as isolation, home quarantine, masks, and social distancing, to target the spread of the disease effectively until a treatment or a vaccine is available for the entire population.

For example, sneezing and coughing are common symptoms of a cold; handwashing mitigates the germs spread. When there is no treatment available, NPIs are the first line of defense for the people (National Geographic Society, 2019). With an attempt to contact-trace and identify possible COVID-19 outbreaks, the Puerto Rican government created a non-pharmaceutical, long-term intervention program called the Puerto Rico Municipal Case Investigation and Contact Tracking System Response to COVID-19 (SMICRC, for its initials in Spanish), whose primary objective is to cut the transmission chains by tracking Covid-19 cases.

Background

Mathematical models help scientists understand how a disease spreads in a susceptible population. Learning about the disease's biology, transmission, and its effect on the population allows determination or prediction of its dynamics (Brauer et al. 2020). Mathematical models have epidemiological classes that help model the disease based on the characteristics exhibited by the virus. Epidemiological classes determine the state or status where the individual is in. The proposed model can be better understood parting from a simple SIR model presenting three initial epidemiological states: Susceptible, Infected, and Recovered (Blackwood et al., 2018). Specific parameters and characteristics that identify the disease determine the individual's condition status (epidemiological state).

Susceptible includes individuals prone to get infected when exposed to the disease. An Infected individual, who already has the disease, spreads the virus to other individuals, dies, or eventually can recover. The Recovered class corresponds to all the individuals seeking treatment, if available, or those who do not present further symptoms. There is an essential factor that determines the recovery process, which is immunity to the disease. Once the individual recovers from the disease with permanent immunity, they will no longer be susceptible to that specific disease again because the individual produced antibodies to the antigen (CDC, 2020a). If the individual does not gain permanent immunity, they return to the Susceptible class.

Methodology

Figure 1 shows the proposed COVID-19 model. It consists of six epidemiological classes: Susceptible (Eq.1), Exposed (Eq.2), Infected (Eq.3), Asymptomatic (Eq.4), Hospitalized (Eq.5) and Convalescent (Eq.6) (SEIAHC Model). This model considers susceptible individuals (S) who can get infected after being exposed (E) to an infected symptomatic (I) or an infected asymptomatic (A). Once the individual changes to the convalescent class (C), a certain immunity is assumed. Additionally, hospitalized individuals (H) are prone to die from COVID-19. Resulting in six ordinary differential equations (ODE) that will help solve the model; Table 1 details each parameter.

This mathematical model allows the study of interactions between each of the epidemiological states. It can adjust to specific populations such as age range, gender, or region. The model incorporates an epsilon parameter, known as the protective rate, to represent all interventions taken. Taking no interventions would present a protective rate with a value of 1. Once the mathematical model incorporates the protective rate, the mitigation strategies can be studied individually to test the magnitude of their effects. The value of this parameter will fluctuate depending on the intervention studied.

To measure the COVID-19 epidemic course and transmission potential, the ODE system must be solved and the Basic (R₀) and Effective (R_e) Reproductive numbers calculated. The R₀ is the number of secondary infections produced in an entirely susceptible population by an infected individual during their infectious period (Montesinos-López et al., 2007). If the value of R₀ equals one or surpasses this value, the epidemic develops. Otherwise, if R₀ is lower than 1, the infection does not become an epidemic, and it is expected to eventually die out (van den Driessche, 2017). ODEs help determine the exact value of the R₀ for the specific model and parameters used in the compartmental model.

To compute the R₀ the second-generation operator is used. Vector F is the rate of new infections going to the latent compartment and vector V the transfer rate of individuals out of the compartment that can transmit the disease. Subsequently, R₀ is the spectral radius of the second-generation operator 𝜌 ( 𝔉𝔙 ^-1 ) also known as the dominant eigenvalue of the matrix 𝔉𝔙 ^-1. Then the dominant eigenvalue of 𝔉𝔙 ^-1 is 𝜌 ( 𝔉𝔙 ^-1 ) which means that the basic reproductive number is:

The R_e is the “expected number of new infections caused by an infectious individual in a population where some individuals may no longer be susceptible” during an epidemic (Gostic et al. 2020). It is given by R₀ at the beginning of the epidemic per the fraction of the population that is susceptible at a time t:

Results & Discussion

This section discusses the findings of the R_e and the explored scenarios. Figure 3 shows the R_e decreasing as the epidemic curve progresses; when a mitigation strategy is applied, the R_e decreases at a faster rate due to the removal of susceptible people from the susceptibility pool. The probability of infection decreases, simultaneously decreasing the case prevalence as people continue taking precautionary measures like social distancing, hand washing, and mask usage. The evident mitigation strategy demonstrated in Figure 3 is the implementation of vaccines in mid-December; this causes the decline in R_e at a much faster rate because of the increased removal of susceptible individuals. The drastic decrease between days 325 to 397 proves the direct relationship between mitigation strategies and R_e's behavior.

Figure 3: Puerto Rico COVID-19 Active Cases and the Re progression

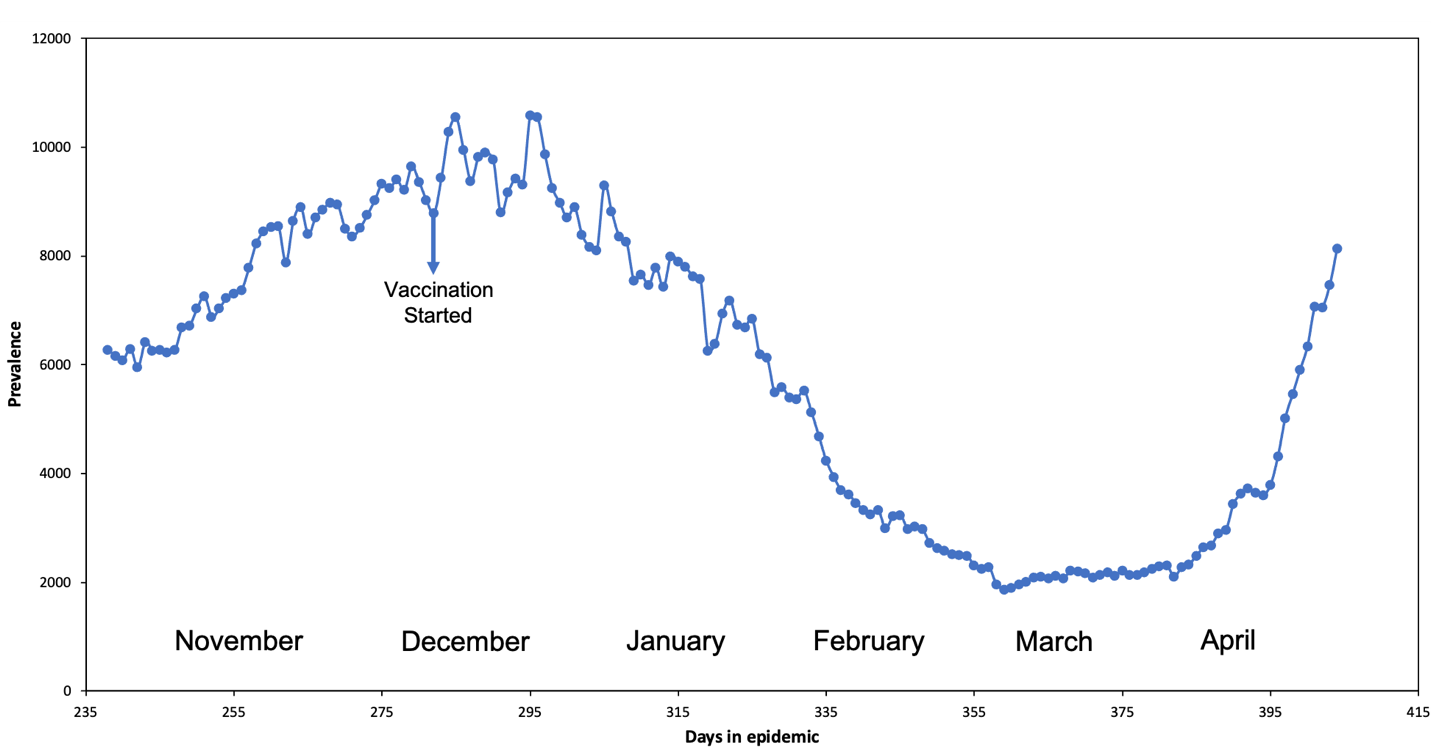
Additional to the vaccination effects on the R_e decline, mask usage is actively present in the mitigation strategies used alongside the novel vaccines. Recognizing the active use of masks is essential because these prove to be effective in decreasing the number of susceptible individuals and consequently decreasing the number of hospitalizations and deaths. Masks continuously show they are an effective and crucial part of controlling the COVID-19 epidemic. "Broad adoption of even relatively ineffective face masks may meaningfully reduce community transmission of COVID-19 and decrease peak hospitalizations and deaths" (Eikenberry et al., 2020). When adoption is nearly universal (nation-wide), and compliance is high, there is a community-wide benefit when referring to interrupting the virus's transmission chains, Figure 4 demonstrates such a decrease.

Figure 4: Vaccination effects on the epidemic curve

It is essential to point out that the behavior of the epidemic curve will directly depend on human behavior and not necessarily on the closure or opening of places. The individual's aleatory behavior cannot be measured; therefore, the model does not consider it.

Conclusion

Mathematical models are tools that help understand the biology of a disease and its transmission throughout a population. It is important to notice that the R_e decreases by taking precautionary and protective measures, minimizing the epidemic. Mitigation strategies such as social distancing and mask usage prevent new infections and maintain a manageable prevalence, preventing a collapse in the healthcare system. The correct implementation of these measures will lead to the controlling and possible eradication of the virus. Reinforcing non-pharmaceutical interventions, social-distancing, and mask usage until 75% or more of the population is fully vaccinated is entirely necessary at this time. The Puerto Rican Government has implemented both suppression and mitigation strategies in response to COVID-19 (PDOH, 2020a). As the COVID-19 pandemic continues, it is aimed to study more mitigation strategies, incorporate them on the model, and run simulations to see the effect on the epidemic curve, resulting in public health policy development to safeguard citizen lives.

Acknowledgements

Thanks to Dr. Mayteé Cruz Aponte for giving us the opportunity to work in her Biomathematics research Lab and being our mentor, the UPR-Cayey, the Interdisciplinary Research Institute, UPR-IPERT (Enhancing Research Training through Empowerment, Resilience, and Civic Engagement) US NIH Grant Award 1 R25 GM121270-01 and the PRLSAMP (Puerto Rico Louis Stokes Alliance for Minority Participation) NSF-HRD 2008186 Grant for supporting this research work.

References

Blackwood, J., & Childs, L. (2018). An Introduction to Compartmental Modeling for the Budding Infectious Disease Modeler. Letters in Biomathematics, 5(1), 195–221. https://doi.org/10.30707/LiB5.1Blackwood

Brauer, F., Castillo-Chávez, C., De La Pava, E., Barley, K., Castillo-Garsow, C., Chowell, D., Espinoza, B., González, P., Hernández, C., & Moreno, V. (2015). Modelos de la propagación de enfermedades infecciosas (pp. 19–31). Universidad Autónoma de Occidente.

CDC. (2020a, February 11). Coronavirus Disease 2019 (COVID-19). Centers for Disease Control and Prevention. https://www.cdc.gov/coronavirus/2019-ncov/more/scientific-brief-sars-cov-2.html

CDC. (2020b, April 27). Nonpharmaceutical Interventions (NPIs). Centers for Disease Control and Prevention. https://www.cdc.gov/nonpharmaceutical-interventions/index.html

CDC. (2021, March 19). COVID-19 Pandemic Planning Scenarios. Centers for Disease Control and Prevention. https://www.cdc.gov/coronavirus/2019-ncov/hcp/planning-scenarios.html

Eikenberry, S., Mancuso, M., Iboi, E., Phan, T., Eikenberry, K., Kuang, Y., Kostelich,E., & Gumel, A. (2020). To mask or not to mask: Modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic. Infectious Disease Modelling, 5, 293–308. https://doi.org/10.1016/j.idm.2020.04.001

Ferguson, N., Laydon, D., Nedjati-Gilani, G., Imai, N., Ainslie, K., Baguelin, M., Bhatia, S., Boonyasiri, A., Cucunubá, Z., Cuomo-Dannenburg, G., Dighe, A., Dorigatti, I., Fu, H., Gaythorpe, K., Green, W., Hamlet, A., Hinsley, W., Okell, L., Elsland, S., . . . Ghani, A. (2020). Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Imperial College COVID-19 Response Team. https://doi.org/10.25561/77482

Gostic, K. M., McGough, L., Baskerville, E. B., Abbott, S., Joshi, K., Tedijanto, C., Kahn, R., Niehus, R., Hay, J., De Salazar, P. M., Hellewell, J., Meakin, S., Munday, J., Bosse, N. I., Sherratt, K., Thompson, R. N., White, L. F., Huisman, J. S., Scire, J., . . . Cobey, S. (2020). Practical considerations for measuring the effective reproductive number, Rt, 16(12). https://doi.org/10.1371/journal.pcbi.1008409

Han, H., Xu, Z., Cheng, X., Zhong, Y., Yuan, L., Wang, F., Li, Y., Liu, F., Jiang, Y., Zhu, C., & Xia, Y. (2020). Descriptive, retrospective study of the clinical characteristics of asymptomatic COVID-19 patients. MSphere, 5(5). https://doi.org/10.1128/mSphere.00922-20

Harvard Health Publishing. (2021). Treatments for COVID-19. Harvard Medical School. https://www.health.harvard.edu/diseases-and-conditions/treatments-for-covid-19

Lotfi, M., Hamblin, M. R., & Rezaei, N. (2020). COVID-19: Transmission, prevention, and potential therapeutic opportunities. Clinica Chimica Acta; International Journal of Clinical Chemistry, 508, 254–266. https://doi.org/10.1016/j.cca.2020.05.044

Montesinos-López, O. A., & Hernández-Suárez, C. M. (2007). Modelos matemáticos para enfermedades infecciosas. Salud Pública de México, 49(3). 218–226. http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S0036-36342007000300007

National Geographic Society. (2019, May 23). Preventing and Containing Outbreaks. National Geographic Society. https://www.nationalgeographic.org/article/preventing-containing-outbreaks/.

Puerto Rico Department of Health. (2021). Dashboard Puerto Rico. Departamento de Salud de Puerto Rico: https://covid19datos.salud.gov.pr

Puerto Rico Department of Health. (2020a). Preventing Measures. Coronavirus. http://www.salud.gov.pr/Pages/Medidas_de_Prevencion.aspx

Puerto Rico Department of Health. (2020b, April 24). Positive Cases COVID-19 Reports from April 24,2020 Until Now. http://www.salud.gov.pr/Estadisticas-Registros-y-Publicaciones/Pages/COVID-19.aspx

van den Driessche, P. (2017). Reproduction numbers of infectious disease models. Infectious Disease Modelling, 2(3), 288–303. https://doi.org/10.1016/j.idm.2017.06.002

Wang, H., Li, X., Li, T., Zhang, S., Wang, L., Wu, X., & Liu, J. (2020). The genetic sequence, origin, and diagnosis of SARS-CoV-2. European Journal of Clinical Microbiology & Infectious Diseases, 39(9), 1629–1635. https://doi.org/10.1007/s10096-020-03899-4

WHO. (2020a, April 27). Archived: WHO Timeline COVID-19. World Health Organization. https://www.who.int/news-room/detail/27-04-2020-who-timeline---covid-19

WHO. (2020b, July 9). Transmission of SARS-CoV-2: implications for infection prevention precautions. World Health Organization. https://www.who.int/news-room/commentaries/detail/transmission-of-sars-cov-2-implications-for-infection-prevention-precautions

WHO. (2020c). Coronavirus Symptoms. World Health Organization. https://www.who.int/health-topics/coronavirus#tab=tab_3

Wiersinga, W. J., Rhodes, A., Cheng, A. C., Peacock, S. J., & Prescott, H. C. (2020). Pathophysiology, transmission, diagnosis, and treatment of Coronavirus disease 2019 (COVID-19): A review. JAMA: The Journal of the American Medical Association, 324(8), 782–793. https://doi.org/10.1001/jama.2020.12839

Worldometer. (2021). Coronavirus Update (Live). COVID-19 Coronavirus Pandemic. https://www.worldometers.info/coronavirus/

Wu, S.-C. (2020). Progress and concept for COVID-19 vaccine development. Biotechnology Journal, 15(6). https://doi.org/10.1002/biot.202000147

Descarga versión pdf

Association between mitigation strategies on the COVID-19 pandemic in Puerto Rico using an epidemiological mathematical model

Contáctanos